Las fracciones expresan la idea de dividir un todo en partes iguales y tomar algunas de ellas.
Dada una fracción ,
 Una fracción también representa el cociente de dos números.
Una fracción también representa el cociente de dos números.
El ejemplo clásico es el de un queso que partimos en porciones iguales. En el dibujo, hemos hecho 8 porciones, 3 rosas y 5 verdes.
Las partes que tomamos (3 ó 5) se llaman numerador y las partes en que dividimos el queso (8) denominador.
Para leer una fracción, el numerador se lee normalmente pero, como veremos a continuación, el denominador tiene una forma especial de leerse.
Los divisores de 42 (Números que dividen exactamente a 42) son:
Cuando en una fracción, el numerador y el denominador no tienen ningún divisor común, se dice que es una fracción irreducible.
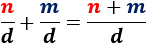
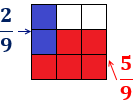
La resta de dos fracciones con denominador común se calcula restando sus numeradores:
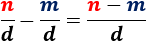
La resta de (cinco novenos) menos (dos novenos) es (un tercio):
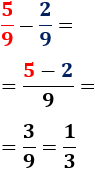 En el último paso hemos dividido numerador y denominador entre 3( fracción equivalente)
En el último paso hemos dividido numerador y denominador entre 3( fracción equivalente)
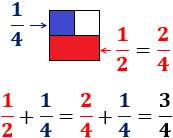
La fracción es igual a la fracción (se observa perfectamente en la representación). Si usamos esta fracción en lugar de , tenemos denominador común y podemos sumar las fracciones fácilmente.
Luego, lo que tenemos que hacer es cambiar una o ambas fracciones por fracciones equivalentes de forma que ambas tengan el mismo denominador.
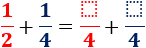
Los numeradores se calculan dividiendo el nuevo denominador entre el antiguo y multiplicando el resultado por el antiguo numerador:

Parece complicado, pero es muy sencillo.
4 : 2 x 1 = 2 4 : 4 x 1 = 1
La división de fracción se calcula multiplicando numerador y denominador en cruz:
Calcular los 2 / 3 de 60:
Dada una fracción ,
- es el numerador
- es el denominador

El ejemplo clásico es el de un queso que partimos en porciones iguales. En el dibujo, hemos hecho 8 porciones, 3 rosas y 5 verdes.
Si tomamos las 3 rosas, representan 3 porciones de las ocho en las que hemos dividido el queso, es decir 3 / 8 del queso, y si tomamos las 5 verdes, representan 5 porciones de las ocho en las que hemos dividido el queso, es decir 5 / 8 del queso.


Las partes que tomamos (3 ó 5) se llaman numerador y las partes en que dividimos el queso (8) denominador.
Para leer una fracción, el numerador se lee normalmente pero, como veremos a continuación, el denominador tiene una forma especial de leerse.
| Denominador y Lectura | Ejemplos | ||
|---|---|---|---|
| 2 | medios | 5/2 | cinco medios |
| 3 | tercios | 2/3 | dos tercios |
| 4 | cuartos | 3/4 | tres cuartos |
| 5 | quintos | 4/5 | cuatro quintos |
| 6 | sextos | 5/6 | cinco sextos |
| 7 | séptimos | 6/7 | seis séptimos |
| 8 | octavos | 7/8 | siete octavos |
| 9 | novenos | 8/9 | ocho novenos |
| 10 | décimos | 9/10 | nueve décimos |
Cuando el Denominador es mayor de 10, se agrega al número la terminación avos.
10 / 11 diez onceavos; 9 / 15 nueve quinceavos.
10 / 11 diez onceavos; 9 / 15 nueve quinceavos.
Clasificación de las Fracciones
Las fracciones se pueden clasificar de distintas formas; en la siguiente tabla se muestran las características de las más importantes.| Tipo | Características | Ejemplos |
|---|---|---|
| Propia | El numerador es menor que el denominador. | 1/2, 7/9 |
| Impropia | El numerador es mayor que el denominador. | 4/3, 5/2 |
| Homogéneas | Tienen el mismo denominador. | 2/5, 4/5 |
| Heterogéneas | Tienen distinto denominador. | 3/7, 2/8 |
| Entera | El numerador es igual al denominador; representa un entero. | 6/6 = 1 |
| Equivalentes | Cuando tienen el mismo valor. Dos fracciones son equivalentes si son iguales sus productos cruzados. | 2/3 y 4/6 2x6=3x4 |
Fracciones equivalentes
Si en una fracción multiplicamos o dividimos el numerador y el denominador por un mismo numero, obtenemos una fracción equivalente a la primera, pues ambas tienen el mismo valor.| 1 | (1 x 4) | 4 | 3 | (3 : 3) | 1 | |||||||||
| — | = | ——— | = | — | = | 0,5 ; | — | = | ——— | = | — | = | 0,2 | |
| 2 | (2 x 4) | 8 | 15 | (15 : 3) | 5 |
Simplificar o Reducir fracciones
Simplificar una fracción consiste en hallar la fracción equivalente más pequeña posible; para ello, lo primero que hacemos es buscar el mayor número que divide exactamente (resto = 0) al numerador y al denominador (mayor divisor común) y después dividimos el numerador y el denominador por este mayor divisor común, y obtenemos una fracción equivalente (de igual valor).Simplificar 30/42
Los divisores de 30 (Números que dividen exactamente a 30) son:
2, 3, 5, 6, 10 y 15.
Los divisores de 42 (Números que dividen exactamente a 42) son:
2, 3, 6, 7, 14 y 21.
Los divisores comunes a ambos son 2, 3 y 6. El mayor divisor común es 6, por tanto, dividimos numerador y denominador por 6.| 30 | 30/6 | 5 | ||
| — | = | —— | = | — |
| 42 | 42/6 | 7 |
Suma y Resta de Fracciones
Si las fracciones tienen el mismo denominador (homogéneas), se suman o restan los numeradores y se pone el mismo denominador.| 3 | 2 | (3 + 2) | 5 | 5 | 2 | (5 - 2) | 3 | |||||||
| — | + | — | = | ——— | = | — | ; | — | - | — | = | ——— | = | — |
| 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 |
Suma:
Cuando dos fracciones tienen el mismo denominador, su suma se calcula sumando los numeradores: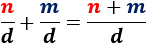
¡Los denominadores no se suman!
La resta de dos fracciones con denominador común se calcula restando sus numeradores:
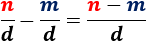
La resta de (cinco novenos) menos (dos novenos) es (un tercio):
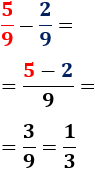
Suma y resta de fracciones con distinto denominador
Suma:
Si los denominadores son distintos, la suma no se calcula simplemente sumando sus denominadores. Por ejemplo, consideremos las fracciones y :
Luego, lo que tenemos que hacer es cambiar una o ambas fracciones por fracciones equivalentes de forma que ambas tengan el mismo denominador.
Método
Para hacer esto, escribiremos como nuevo denominador al mínimo común múltiplo de los dos denominadores:
Los numeradores se calculan dividiendo el nuevo denominador entre el antiguo y multiplicando el resultado por el antiguo numerador:

Parece complicado, pero es muy sencillo.
Resta:
Para calcular la resta, procedemos del mismo modo, pero restando los numeradores en el paso final.
Calcular las siguientes sumas de fracciones con denominador distinto:
Solución
El mínimo común múltiplo de y es . Por tanto, tenemos
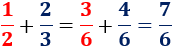
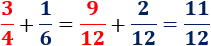
El mínimo común múltiplo de y
es
. Por tanto, tenemos
El mínimo común múltiplo de y es . Por tanto, tenemos
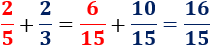
Solución
El mínimo común múltiplo de y es . Por tanto, tenemos
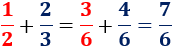
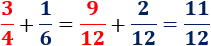
El mínimo común múltiplo de y es . Por tanto, tenemos
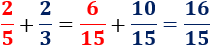
Calcular la siguiente resta de fracciones con denominador distinto:
El mínimo común múltiplo de
y
es
. Por tanto, tenemos
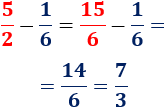
La multiplicación de fracciones
Es muy fácil de calcular y no importa si tienen denominador común o no:
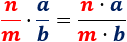 Es decir, se multiplican los numeradores y los denominadores.
Es decir, se multiplican los numeradores y los denominadores.
Por ejemplo,
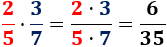
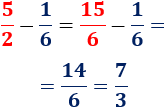
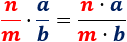
Por ejemplo,

División de fracciones
La división de fracción se calcula multiplicando numerador y denominador en cruz:
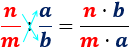 Por ejemplo,
Por ejemplo,
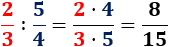 Es decir,
Es decir,
- El numerador es el producto del numerador de la primera fracción y del denominador de la segunda.
- El denominador es el producto del denominador de la primera fracción y del numerador de la segunda.
También, podemos escribir la división como
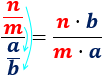 Regla que suele ayudar: el de arriba ( ) por el de abajo ( ) entre los dos del medio ( y ).
Regla que suele ayudar: el de arriba ( ) por el de abajo ( ) entre los dos del medio ( y ).
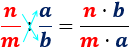
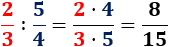
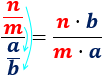
Fracción de un Número
Calcular la fracción de un número es lo mismo que multiplicar la fracción por ese número.Calcular los 2 / 3 de 60:
| 2 | 2 | (2 x 60) | 120 | |||||||||
| — | de | 60 | = | — | x | 60 | = | ——— | = | —— | = | 40 |
| 3 | 3 | 3 | 3 |
No hay comentarios:
Publicar un comentario