En esta secuencia didáctica se tratarán aspectos importantes sobre el género periodístico de carácter interpretativo: la entrevista. Se conocerá desde el concepto de entrevista, hasta cuál es su estructura y contenido, cómo se planifica y cómo se realiza. A través de las actividades propuestas se realizarán algunas entrevistas que permitirán poner en práctica lo aprendido y conocer todo lo necesario sobre las mismas.
Etiquetas
Etiquetas
viernes, 7 de diciembre de 2018
Giros
Ángulos y giros de 90º
El giro, también se llama rotación, es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original.

Una rotación se determina por estos tres elementos:
El giro de 90 grados es muy común. Si marcamos 90º y vamos añadiendo cada vez 90º obtenemos cuatro ángulos muy comunes que debes aprender.

Si consideramos el movimiento podemos decir que en cada uno de estos giros la flecha se ha movido: 90º, 180º, 270º y 360º a la izquierda (sentido contrario a las agujas del reloj)
Si añadimos 45º, y giramos en sentido de las agujas del reloj, obtendremos estos ángulos para indicar la dirección de los puntos cardinales básicos. (Consideramos 0º a la orientación Norte)

Una rotación se determina por estos tres elementos:
- Un ángulo que determina la amplitud de la rotación.
- Un punto llamado centro de rotación.
- Un sentido de la rotación que puede:
- A la derecha: en el mismo sentido que las agujas del reloj.
- A la izquierda: en el sentido contrario a las agujas del reloj.
El giro de 90 grados es muy común. Si marcamos 90º y vamos añadiendo cada vez 90º obtenemos cuatro ángulos muy comunes que debes aprender.


Si consideramos el movimiento podemos decir que en cada uno de estos giros la flecha se ha movido: 90º, 180º, 270º y 360º a la izquierda (sentido contrario a las agujas del reloj)
Si añadimos 45º, y giramos en sentido de las agujas del reloj, obtendremos estos ángulos para indicar la dirección de los puntos cardinales básicos. (Consideramos 0º a la orientación Norte)
- 45º a la derecha: orientación NE
- 90º a la derecha: orientación E
- 135º a la derecha: orientación SE
- 180º a la derecha: orientación S
- 225º a la derecha: orientación SO
- 270º a la derecha: orientación O
- 315º a la derecha: orientación NO
 @lobatez. Ángulos de las posiciones cardinales (Dominio público)
@lobatez. Ángulos de las posiciones cardinales (Dominio público)
Suma y resta de ángulos
Dos ángulos pueden sumarse para formar otro.
Suma gráfica:

Recuerda lo aprendido en la suma en el sistema sexagesimal:
Suma gráfica:

- Se colocan ambos ángulos de manera consecutiva, es decir, compartiendo el vértice y uno de sus lados.
- El ángulo suma de los dos es el ángulo que comprende a ambos.
Recuerda lo aprendido en la suma en el sistema sexagesimal:
- Se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos.
- Se comienza sumando los segundos. Si los segundos resultantes suman más de 60'', el resultado se divide entre 60, el cociente se añade a los minutos y el resto son los segundos.
- Se hace lo mismo con los minutos.
Dos ángulos pueden restarse para formar otro.
Resta gráfica:

Recuerda lo aprendido en la resta en el sistema sexagesimal:
Resta gráfica:

- Se colocan ambos ángulos de manera que coincida el lado origen de cada ángulo y compartiendo el vértice.
- La diferencia entre el ángulo mayor y el menor es el ángulo resta.
Recuerda lo aprendido en la resta en el sistema sexagesimal:
- Se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos.
- Se comienza restando los segundos. Si el minuendo es menor que el sustraendo, se pasa un minuto a segundos para poder hacer la resta.
- Se hace lo mismo con los minutos.
Bisectriz y mediatriz
La recta que divide a un ángulo por la mitad se llama bisectriz:

https://sites.google.com/site/todoesgeometria/construcciones-con-regla-y-compas/hallar-la-bisectriz-de-un-angulo-dado
Aprende a trazarla con el compás:

https://sites.google.com/site/todoesgeometria/construcciones-con-regla-y-compas/hallar-la-bisectriz-de-un-angulo-dado
Aprende a trazarla con el compás:
La mediatriz de un segmento es la recta perpendicular al segmento que pasa por su punto medio.

La mediatriz divide el segmento en dos partes iguales; las dos partes miden lo mismo.
Aprende a trazar la mediatriz con un compás:

La mediatriz divide el segmento en dos partes iguales; las dos partes miden lo mismo.
Aprende a trazar la mediatriz con un compás:
Dibujar un triángulo equilátero
Dibujar un triángulo equilátero es muy sencillo... si tenemos en cuenta que todos los ángulos son iguales y miden 60º (180º:3 = 60º)
Para dibujar un triángulo equilátero que midan sus lados 5 cm sigue estos pasos:
- Dibuja un ángulo de 60º
- Marca en ambos lados del ángulo la distancia, 5 cm.
- Une ambas marcas.
- Comprueba que todos los lados miden 5 cm y los ángulos 60º

Ángulos

Los ángulos se pueden clasificar según la abertura de sus lados:
- Agudos: miden menos de 90º
- Rectos: miden 90º
- Obtusos: miden más de 90º pero menos de 180º
- Llanos: miden 180º
- Mayores de 180º: pues eso, miden más de 180º
- Completos: miden 360º
Experimenta con los ángulos en esta web: http://www.visnos.com/app/basic-angles
Entre 2 ángulos se pueden establecer distintas relaciones:
Ángulos consecutivos: Son aquellos que tienen en común el vértice y uno de los lados.
 Los ángulos A y B son consecutivos y juntos suman lo mismo que el ángulo C.
Los ángulos A y B son consecutivos y juntos suman lo mismo que el ángulo C.
Hay dos casos especiales de ángulos consecutivos, según el ángulo que suman entre ambos:


Ángulos consecutivos: Son aquellos que tienen en común el vértice y uno de los lados.
 Los ángulos A y B son consecutivos y juntos suman lo mismo que el ángulo C.
Los ángulos A y B son consecutivos y juntos suman lo mismo que el ángulo C.Hay dos casos especiales de ángulos consecutivos, según el ángulo que suman entre ambos:
- Ángulos complementarios: Son dos ángulos consecutivos que suman 90 grados, formando su unión un ángulo recto.
- La suma de estos dos ángulos forman un ángulo recto (50º + 40º = 90º).

@lobatez. Ángulos complementarios y suplementarios (Dominio público)
- Ángulos suplementarios: Son dos ángulos consecutivos que suman 180 grados, formando su unión un ángulo llano.
- La suma de estos dos ángulos forman un ángulo llano (130º + 50º = 180º).

Tiempo
 En el Sistema Internacional la unidad fundamental de medida del tiempo es el segundo.
En el Sistema Internacional la unidad fundamental de medida del tiempo es el segundo.Los múltiplos del segundo son el minuto y la hora (ver unidades del sistema sexagesimal)
Estas tres unidades forman el sistema sexagesimal con el que expresamos las medidas del tiempo en nuestra vida cotidiana.
- El segundo se escribe s
- El minuto se escribe min
- La hora se escribe h
- 1 día = 24 horas.
- 1 semana = 7 días.
- 1 mes = 28, 29, 30 o 31 días.
- 1 trimestre = 3 meses.
- 1 cuatrimestre = 4 meses.
- 1 semestre = 6 meses.
- 1 año = 365 días (366 si es bisiesto).
- 1 lustro o quinquenio = 5 años.
- 1 década = 10 años.
- 1 siglo = 100 años.
- 1 milenio = 1.000 años.
En el sistema sexagesimal el tiempo se escribe separando las cifras que corresponden a horas, minutos y segundos por dos puntos.
La cifra de los minutos y segundos debe llevar dos dígitos:

La cifra de los minutos y segundos debe llevar dos dígitos:
- 12:03:45 se lee: 12 horas, 3 minutos y 45 segundos.
- 7:53:27 se lee: 7 horas, 53 minutos y 27 segundos

El calendario es un sistema por el que se asigna a cada día una fecha formada por tres datos: número del día, número del mes y número del año. 17 – 03 – 1940 día 17 del mes de marzo del año 1940.
No todos los países usan el mismo calendario.

El reloj es el principal instrumento de medida del tiempo y puede ser de diferentes tipos.
Los relojes de agujas nos marcan el transcurso del tiempo por el giro de las agujas en la esfera del reloj y podemos leerlo interpretando el ángulo que forman. Sólo marcan 12 horas; por eso tenemos que aclarar si son de la mañana (a.m.) o de la tarde (p.m.). El reloj siguiente representa 9 h 10 min y 30 s, también podemos escribirlo así: 09:10:30, pero no sabemos si es de la mañana o de la noche.

No todos los países usan el mismo calendario.
- El calendario gregoriano o cristiano cuenta los años a partir del nacimiento de Jesucristo. La fecha se expresa poniendo 25 a. C o 540 d. C.
- El calendario judío se inicia el año 3761 a. C.
- El islámico, el año 622 d. C. y sus años tienen 354 días.
- Se observa la cifra de las centenas y se le suma 1.
- El siglo siempre se escribe con números romanos.
- En el gráfico siguiente, se muestran algunos ejemplos prácticos para realizar estos cálculo

El reloj es el principal instrumento de medida del tiempo y puede ser de diferentes tipos.
- En la antigüedad se usaban los relojes de sol y de arena, después se usó el de péndulo.
- Más moderno es el de cuerda.
- En la actualidad suelen funcionar con pilas y las horas las marcan usando agujas o son digitales.
Los relojes de agujas nos marcan el transcurso del tiempo por el giro de las agujas en la esfera del reloj y podemos leerlo interpretando el ángulo que forman. Sólo marcan 12 horas; por eso tenemos que aclarar si son de la mañana (a.m.) o de la tarde (p.m.). El reloj siguiente representa 9 h 10 min y 30 s, también podemos escribirlo así: 09:10:30, pero no sabemos si es de la mañana o de la noche.

Suma y resta en el sistema sexagesimal
La suma con unidades sexagesimales es sencilla.

- Se colocan verticalmente las unidades de cada clase alineando las horas o grados con las horas o grados, los minutos con los minutos y los segundos con los segundos. Hecho esto se suma.
- Si al sumar los segundos el resultado es mayor que 60 se divide entre 60, el cociente se añade a los minutos y el resto queda como segundos.
- Se hace lo mismo con los minutos.
Por ejemplo: 234º 34' 26" + 12º 47' 53" = 247º 22' 19"

@lobatez (Dominio público)
Para restar se procede igual.

- Se escriben las medidas de manera que coincidan en columnas las unidades del mismo orden y se restan.
- Si al restar los segundos es menor el minuendo, convertimos un minuto del minuendo en segundos y sumamos 60" al orden de los segundos.
- Se hace lo mismo con los minutos.
Por ejemplo: 28º 32' 23" - 13º 54' 24" = 14º 37' 59"

@lobatez (Dominio público)
jueves, 6 de diciembre de 2018
Sistema sexagesimal

Expresiones como estas son frecuentes escucharlas en las conversaciones y en las noticias: "quedamos a las 7 h y 32 min", "el ángulo de apertura es de 90º", "el ángulo complementario sumaba 36º", "la ceremonia comenzó a las doce y cuarto", "la pelota trazó un ángulo de 60º al chocar contra el larguero", "el tren llegó con media hora de retraso", "Kipsang recorrió los 42,195 kilómetros de la Marathon en 2:02:57 horas", "se localizó el avión siniestrado cerca de las Islas Salomón en 10° 40' 17'' S 160° 7' 57'' E", "el colegio Manuel Bartolomé Cossío está situado en las coordenadas 40° 22′ 52″ N y 03° 46′ 18″ W"...
En todas estas situaciones usamos el sistema sexagesimal.
Este sistema lo usamos para medir tiempos (horas, minutos y segundos), ángulos (grados, minutos y segundos) y coordenadas cartesianas para situar una posición.
El sistema sexagesimal es un sistema de numeración posicional que emplea como base el número 60.
Unidades del sistema sexagesimal
El Sistema Sexagesimal lo utilizaremos en este libro para medir el tiempo y los ángulos.
Es un sistema de numeración de base 60, es decir, cada unidad se divide en 60 unidades de orden inferior.

Es un sistema de numeración de base 60, es decir, cada unidad se divide en 60 unidades de orden inferior.
- 1 grado = 60 minutos, también 1 hora = 60 minutos.
- 1 minuto = 60 segundos.
| Ángulos | grados | minutos | segundos |
| Abreviatura | º | ' | " |
| Conversión | 1º | 1º = 60' | 1º = 3.600" |
| Tiempo | horas | minutos | segundos |
| Abreviatura | h | min | s |

@lobatez (Dominio público)
Igual que con el Sistema Métrico Decimal es importante tener una tabla, en este caso sexagesimal, para hacer las conversiones.
Es el mismo procedimiento para las unidades de ángulos que para las de tiempo, solo hay que poner la abreviatura correspondiente:
Pasar a unidades menores: "nos desplazamos a la derecha" y multiplicamos cada salto por 60.
Es el mismo procedimiento para las unidades de ángulos que para las de tiempo, solo hay que poner la abreviatura correspondiente:
Pasar a unidades menores: "nos desplazamos a la derecha" y multiplicamos cada salto por 60.
- Convertir grados (horas) a minutos: multiplicamos por 60 (un salto a la derecha)
- 23º son 23 x 60 = 1.380'
- 3 h son 3 x 60 = 180 min.
- Convertir grados (horas) a segundos: multiplicamos por 3.600 (dos saltos a la derecha)
- 12 h son 12 x 3.600 = 43.200 s
- 35º son 35 x 3.600 = 126.000"
Expresión simple: utilizamos un solo tipo de unidad para expresar la medición
- 3 h.
- 254 s.
- 34'
Expresión compleja: utilizamos varias unidades para expresar la medida.
- 34 h 54 min
- 134º 16' 23"
Paso de expresiones complejas a simples:
Se pasa cada unidad al tipo que deseamos y se suman. Vamos a estudiar dos casos:
- Expresar en minutos:
- 8 h 36 min = 8 x 60 + 36 = 480 + 36 = 516 min
- Expresar en segundos:
- 24º 32' 16" = 24 x 3.600 + 32 x 60 + 16 = 86.400 + 1.920 + 16 = 88.336"
Paso de expresiones simples a complejas.
Lo estudiaremos para pasar de una unidad menor a otra mayor.
En este caso "nos desplazamos a la izquierda" por lo que dividimos cada "salto" entre 60.
Al no ser un sistema decimal, si la división es entera el resto se expresa tal cual, indicando los minutos o segundos que nos han sobrado de resto. Fíjate en el ejemplo:
- Convertir minutos en horas o grados: dividimos por 60 (un salto a la izquierda)
- 360 min calculamos 360 : 60 = 6 h (justas porque la división es exacta)
- 385 min calculamos 385 : 60 = 6 h 25 min (porque el resto es 25)
- 1.643' calculamos 1.643 : 60 = 27º 23" (porque el resto es 23)

@lobatez (Dominio público)
- Convertir segundos en minutos y horas (o grados): hacemos dos divisiones consecutivas por 60 (dos saltos a la izquierda), en la primera división obtenemos el resto de segundos y los minutos y en la segunda división el resto de los minutos y las horas (o grados). Observa el esquema:
- 25.486 s = 7 h 04 min 46 s que se obtienen del segundo cociente y los restos de los minutos y segundos.
- 15.654" = 4º 20' 54"

@lobatez (Dominio público)
NÚMEROS ROMANOS
Numeración romana:
Es un sistema de numeración que usa letras mayúsculas a las que se ha asignado un valor numérico.
Este tipo de numeración debe utilizarse lo menos posible, sobre todo por las dificultades de lectura y escritura que presenta.
Se usa principalmente:
- En los números de capítulos y tomos de una obra.
- En los actos y escenas de una obra de teatro.
- En los nombres de papas, reyes y emperadores.
- En la designación de congresos, olimpiadas, asambleas, certámenes..
Reglas:
| Letras | I | V | X | L | C | D | M |
| Valores | 1 | 5 | 10 | 50 | 100 | 500 | 1.000 |
Ejemplos: XVI = 16; LXVI = 66
Ejemplos: VI = 6; XXI = 21; LXVII = 67
Ejemplos: IV = 4; IX = 9; XL = 40; XC = 90; CD = 400; CM = 900
Ejemplos: XIII = 13; XIV = 14; XXXIII = 33; XXXIV = 34
Ejemplos: X = 10; C = 100; M = 1.000
Ejemplos: XIX = 19; LIV = 54; CXXIX = 129
Ejemplos:  = 1.000.000
= 1.000.000
El Sistema de numeración romano usa letras mayúsculas a las que se ha asignado un valor numérico. Con la tabla de numeración romana podrás encontrar cómo se dice cada numeral romano.

ACTIVIDAD LÚDICA:
El alumno o alumna tendrá que colorear la figura de un romano, valiéndose de sus conocimientos aprendidos en esta unidad.
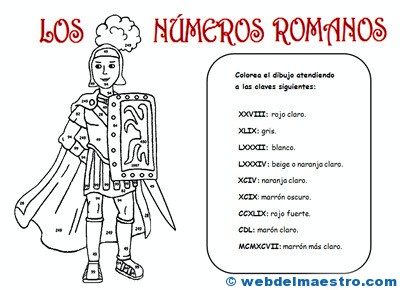

Terminación del trabajo:

Para repasar, jugar y divertirte.
ACTIVIDADES/FICHAS
Fuente: ACTILUDIS
Fuente: ACTILUDIS
 |
| LOS NÚMEROS ROMANOS EN BLANCO Y NEGRO |
 |
| LOS NÚMEROS ROMANOS EN COLOR Fuente: ACTILUDIS |
Fuente: ACTILUDIS
Fuente: Santillana
Fuente: Santillana
Fuente: Menudospeques.net
Fuente: Menudospeques.net
Fuente: Menudospeques.net
Fuente: Menudospeques.net
Fuente: Menudospeques.net
Fuente: Menudospeques.net
Fuente: rinconmaestro.es
ACTIVIDADES PDI
VÍDEOS
Suscribirse a:
Comentarios (Atom)


.jpg)
















